狗亲家
狗亲家
CSP 普及组以前很少在复赛中考树上问题。
直到 2018 年第四题考了《对称二叉树》,2020 年第三题考了《表达式》。
树上问题,是提高组复赛的命题大户,普及组很少涉及。但是随着普及组的题目越来越难,我总觉树上问题有可能会再出现。《狗亲家》的难度介于《对称二叉树》和《表达式》之间,学完树的同学,可以想想怎么解。
题目描述:
一个小镇上有 N 个人,他们之间有 N-1 对相识关系。小镇上的任意两个人,都能通过认识的人最终互相认识。
有一天,张三家的狗和李四家的狗打了一架,张三和李四就不理对方了;这时候小镇上的人就分裂成两个互相不认识的集团了。
又过了一段时间,王五家的狗和赵六家的狗谈朋友,原本互相不认识的王五和赵六也就认识了。他们认识之后,整个小镇上的人又都互相认识了。
请问:故事中的王五和赵六有多少种组合方法?(王五和赵六,也可以是张三和李四,即两只打架的狗,也可以谈朋友。)
输入输出格式:
第一行输入 N,紧接着 N-1 行,每行两个整数,表示互相认识的两个人。
接下来一行是测试组数 K,然后是 K 行,每行两个整数,代表张三和李四的编号。数据保证张三和李四是原来是互相认识的。
要求输出 K 行。每行一个整数,表示对于一组张三和李四,有多少种王五和赵六的组合方式。
样例数据
输入:
6
1 2
1 3
3 4
3 5
6 3
3
1 2
1 3
4 3
输出:
5
8
5
数据范围:
- 50% 的数据 $10 \le N,K \le 10^3$
- 100% 的数据 $10 \le N,K \le 10^6$
题解
题目第一句:“一个小镇上有 N 个人,他们之间有 N-1 对相识关系。小镇上的任意两个人,都能通过认识的人最终互相认识。”
这说明小镇上人们的关系,组成了一棵树。下图上半部分是样例数据中小镇的原始关系图,下半部分,分别代表三组测试中张三和李四断开的关系。
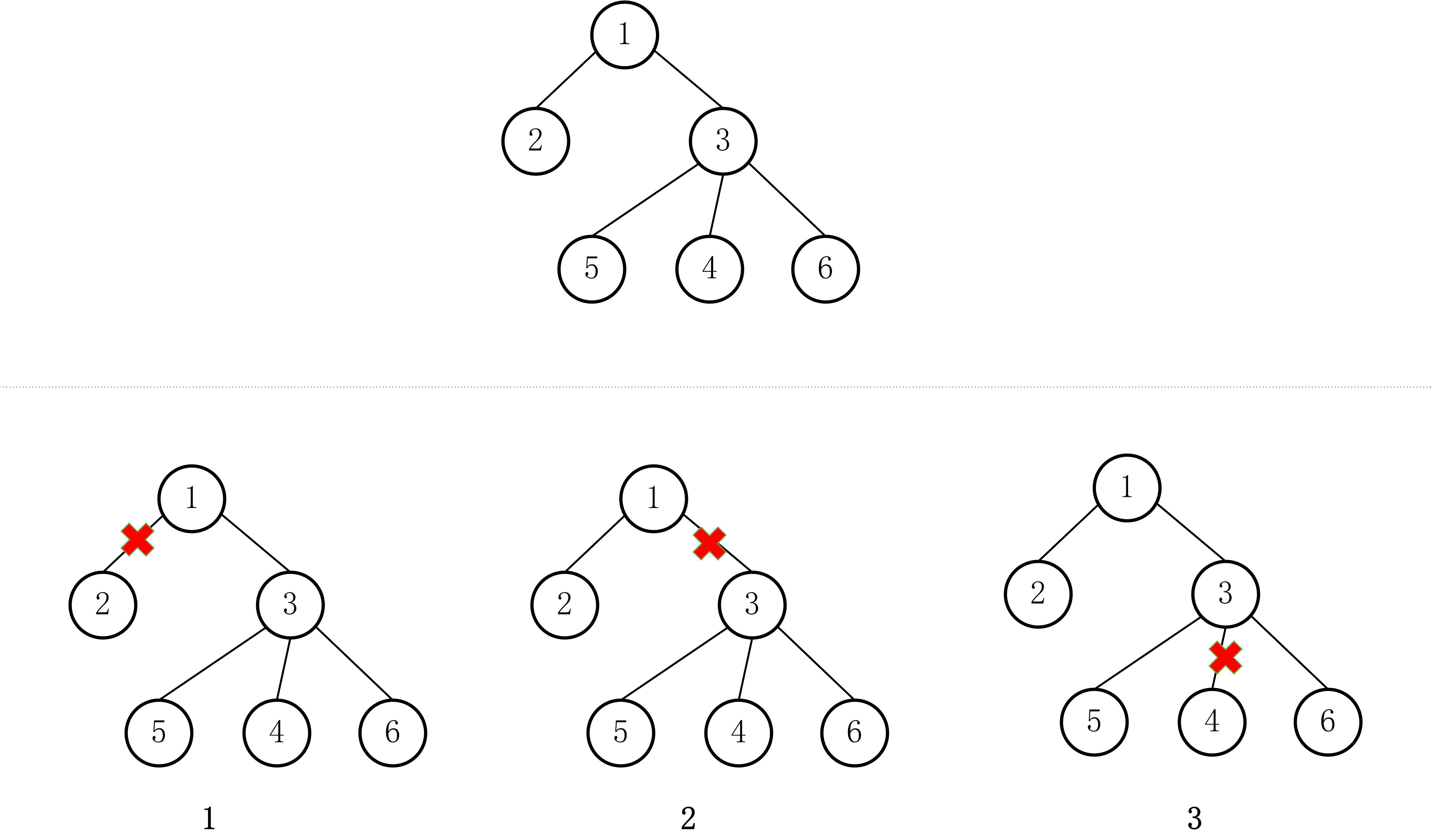
根据组合数学的乘法原理,王五和赵六的组合方式,是断开关系的两部分人群的数量的乘积。
对于第一组测试,王五只能是【2】,赵六可以是【1,3,4,5,6】中的一个,因此有 5 种组合。
对于第二组测试,王五可以是【1,2】当中的一个,赵六可以是【3,4,5,6】中的一个,因此有 $2 \times 4=8$ 种组合。
对于第三组测试,王五可以是【1,2,3,5,6】当中的一个,赵六只能是【4】,因此有 5 种组合。
所以说,只需要知道被张三和李四切开的两个树,各有多少个节点就行了。
具体做法是这样的:
先任取一点为根,DFS 求出每颗子树的节点数目和深度,记下来。我们令 $deep[i]$ 表示节点 $i$ 的深度,$cnt[i]$ 表示以节点 $i$ 为根的子树大小。
然后读取每一组切掉的边的时候,找到子树的根 $i$,计算 $(N-cnt[i]) \times cnt[i]$ 就可以了。
怎么判断切掉的边,哪边是父,哪边是子呢? 可以在 DFS 求子树节点数目的时候,顺便记下来每个节点的深度。深度深的,就是子节点了。 还有一种更省事的方法,就是切掉那个边,父节点的子树节点个数肯定大于子节点的子树节点个数。所以就看谁的子树节点少,就是子节点了。
复杂度:算法复杂度是 $O(N) + O(K)$,满足要求。