分球的八个问题
问题:把 m 个球放入 n 个盒子里,有多少种放法?
这题目其实条件没说清,m 球放 n 盒,可以有 8 种情况:
- 球同,盒同,盒不可以为空
- 球同,盒同,盒可以为空
- 球同,盒不同,盒不可以为空
- 球同,盒不同,盒可以为空
- 球不同,盒同,盒不可以为空
- 球不同,盒同,盒可以为空
- 球不同,盒不同,盒不可以为空
- 球不同,盒不同,盒可以为空
这 8 个问题,看起来相似,但是解法上是有不同的。我们一个一个看。
问题 8:球不同,盒不同,盒可以为空
最简单的,是问题 8:m 不同球,n 不同盒,允许空盒。
每个球都有 n 种选择,m 个球就有 $n^m$ 种分法。
$S1(m,n) = n^m$
问题 2:球同,盒同,盒可以为空
问题 2:m 同球,n 同盒,允许空盒。
分情况讨论:
A,球数 (m) 少于盒子数 (n):则分配方案和 m 个球放入 m 个盒子相同。
B,球数 (m) 不少于盒子数 (n):
可以分解为两种情况:
1,至少有一个空盒子。这种情况,与去掉一个空盒子方案数相同。即:$m$ 个同球放入 $n-1$ 个同盒子,允许空盒的方案。
2,没有空盒子,所有的盒子都至少放一个球,转化为 $m-n$ 个球放入 $n$ 个盒子的方案。
任何一种 $m$ 个同球放入 $n$ 个同盒的方案必然属于上述两种方案之一,既不会同时属于上述两种方案,也不会出现在这两种方案之外。
$S2(m,n) = S2(m, n-1) + S2(m-n,n)$,如果 $m-n < n$,则后一项为 $S2(m-n, m-n)$。
问题 1:球同,盒同,盒不可以空
问题 1:m 同球,n 同盒,无空盒。
既然 m 个球是相同的,而且没有空盒,那从所有方案的每个盒子拿走一个球,方案数不变。
每个盒子拿走一个球,问题 1 转化为 问题 2。
$S1(m,n) = S2(m-n, n)$
问题 3:球同,盒不同,盒不可以空
问题 3:m 同球,n 不同盒,无空盒。
这个问题用组合数学插板法解决。
把 $m$ 个球排成一排(只有一种方法),它们中间有 $m-1$ 个空挡。从 $m-1$ 个空挡中选择 $n-1$ 个,放入插板。每个空挡最多放一个插板,就把 m 个球分成 n 部分。由于插板不相邻,所以没有空盒。
问题 3 的方法数有 $S3(m,n) = C_{m-1}^{n-1}$ 个。
组合数公式:$C_n^r = \frac{P_n^r}{r!} = \frac{n!}{r! \cdot (n-r)!}$ ,$P_n^m = \frac{n!}{(n-m)!}$
问题 4:球同,盒不同,盒可以为空
问题 4:m 同球,n 不同盒,允许空盒。
问题 4 可以通过问题 3 求解。
为了避免空盒,先在每一个盒里假装放一个球,这样就有 $n+m$ 个球。按照问题 3 的方法分完了之后,再从每个盒子里面取走一个球,方案数不变。
问题 4 的方法数是:$S4(m,n) = S3(m+n,n) = C_{n+m-1}^{n-1}$。
问题 5、6、7,先熟悉一下这个三角形:
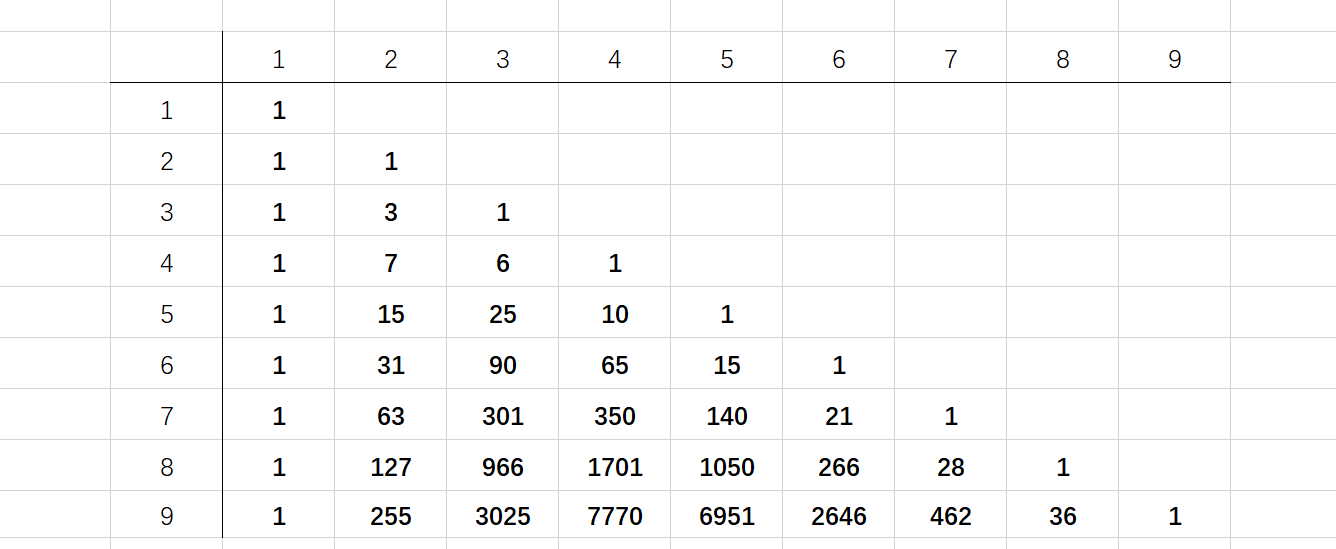
性质1,左右两边都是1,第几行就有几个数,比如第 5 行就是 1 X X X 1。
性质2, $S(N, K) = S(N-1, K-1) + K \times S(N-1, K)$,含义是第 $N$ 排的第 $K$ 个数等于 { 它上一排的左上角位置的数字 } 加 { 它上一排的同样位置数字的 $K$ 倍}。
例如 $S(7, 3)$ 就是第 7 排第 3 个数字,所以他等于第 6 排第 2 个数字 加 第 6 排第 3 个数字乘以 3。
所以第 1 排是1,第2排 1,1,第 3 排(左右两边都是1,只有中间那个数字没确定)。 所以 $S(3, 2) = $第 2 排第 1 个数字 加 第 2 排第 2 个数字的两倍 $= 1+1 \times 2 = 3$,所以第 3 排数字就是 1,3,1。同理 $S(4, 2) = S(3, 1) + 2 \times S(3, 2) = 1+2 \times 3 = 7, … $如此类推。
问题 5,球不同,盒同,盒不可以为空
问题 5:m 不同球,n 同盒,无空盒。
假设 $S5(m,n)$ 为 m 个不同的球,放入 n 个相同的盒子,盒子不可以为空的放法总数。
考虑递推关系。假设 m 个球是依次放入盒子中的,即球是按照 $1,2,3,...,m$ 的顺序放入的。显然,对于一种放法方案,我们固定一个放入顺序并不会增加或者减少方案的数目。 则 $m$ 号球放入之前,有 $m-1$ 个球放入 n 个盒子,方案数为 $S5(m-1,n)$。第 $m$ 号球有 $n$ 种放法(放入 n 个盒子中的任意一个),因此有 $n \times S5(m-1,n)$ 种放法。
上述这种考虑,还缺一个方案,就是 $m$ 号球放入的那个盒子,只有 $m$ 号球。这时候,在 m 号球放入之前,是有空盒子的,这种情况不在 $S5(m-1,n)$ 表达的范围内。因为盒子是相同的,因此在 $m$ 号球放入之前,只有 $n-1$ 个非空的盒子,方案数为 $S5(m-1, n-1)$。
综上,递推公式为:$S5(m,n) = S5(m-1,n-1) + n \times S5(m-1,n)$。
问题6,球不同,盒同,盒子可以为空
问题6:m 不同球,n 同盒,允许空盒(在问题 5 的基础上允许空盒)。
那就枚举空盒子的数量:一个空盒子都没有 + 有一个空盒子 + 有两个空盒子 + 有三个空盒子+ ,,,+都装在一个盒子里。
改写成公式就是:$S6(m,n) = S5(m, 1) + S5(m, 2) + S5(m, 3) + … + S5(m, n)$
也就是上面那个三角形,第 m 排开始第 1 个数字一直加到第 n 个数字。
问题 7,球不同,盒不同,盒不可以为空
问题 7:m 不同球,n 不同盒,无空盒。
问题 7 和问题 5 的区别是,盒子不同。那就先按照问题 5 分,然后把盒子全排列编号就行了。
所以问题 7 的解是:$S7(m,n) = n! \times S5(m, n)$。
总结
输出方案数问题是信息学竞赛中的一种常考题目。
通过【分球的八个问题】,可以帮我们把组合数学的加法原理、乘法原理和动态规划的方案递推思路认真梳理一遍,对锻炼这种题目的思考方法是很有帮助的。